
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구하는 문제
타일 채우기 아우 지겨워~ 하고 풀었다가 멍청한 나한테 질렸다..
모든 예외들을 잘 고려해줘야 한다.
1. N이 홀수일 때
해보면 알겠지만 3x1, 3x3, 3x5 ··· N이 홀수일 땐 채울 수 없다.
2. 3x2
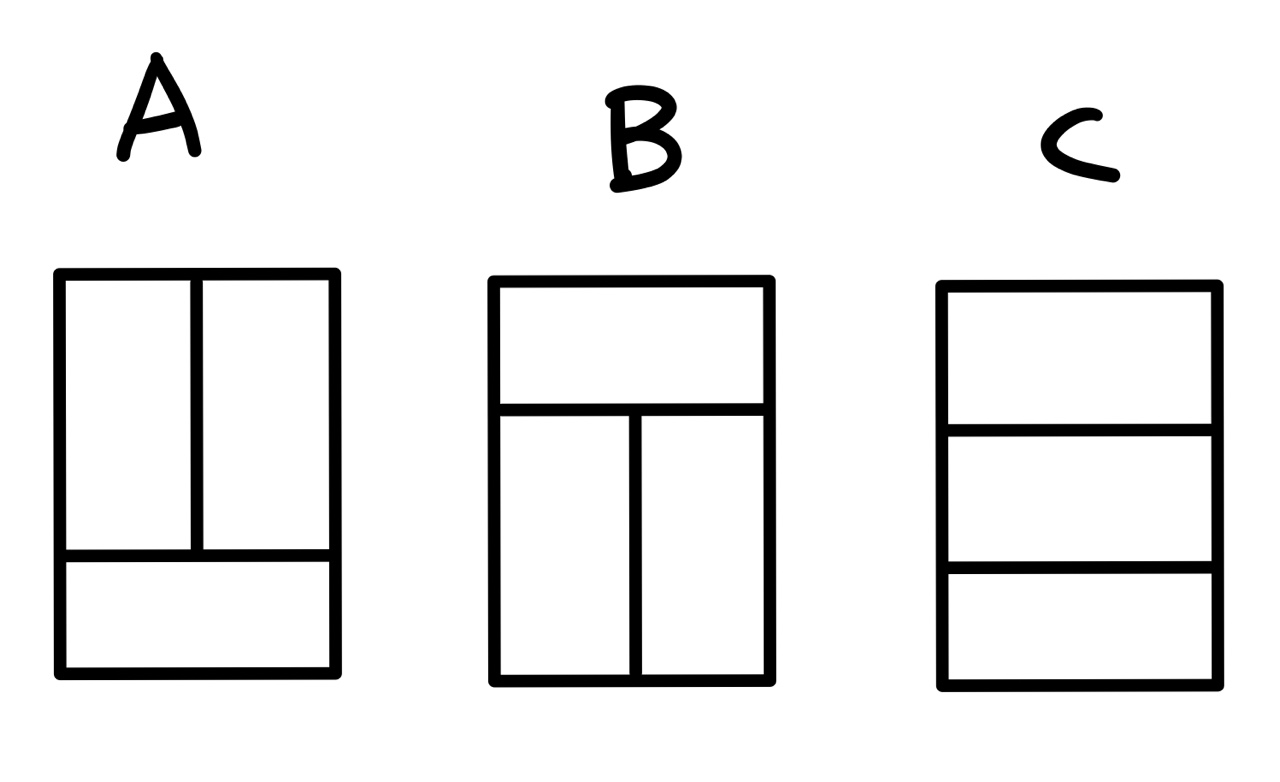
3x2의 경우엔 이렇게 세 가지 모양으로 채울 수 있다.
각각을 A, B, C라 칭하겠음!
3. 3x4

1번에 A, B, C + 2번에 A, B, C를 조합하여 채우는 형태로 생각할 수 있다
이러면 3x3=9, 총 9개의 형태로 채울 수 있다!!
하지만 답은 9가 아니다.
3x4부터 예외가 발생한다...

단순히 A, B, C를 조합해서는 만들 수 없는 모양으로, 3x4부터 이런 형태가 등장한다.
이런 경우를 '특별한 모양'이라고 칭하겠다!!!
즉 3x4는 A, B, C를 조합하여 만든 모양 9개 + 위와 같은 형태 2개 = 총 11개의 경우의 수를 가진다.
4. 3x6
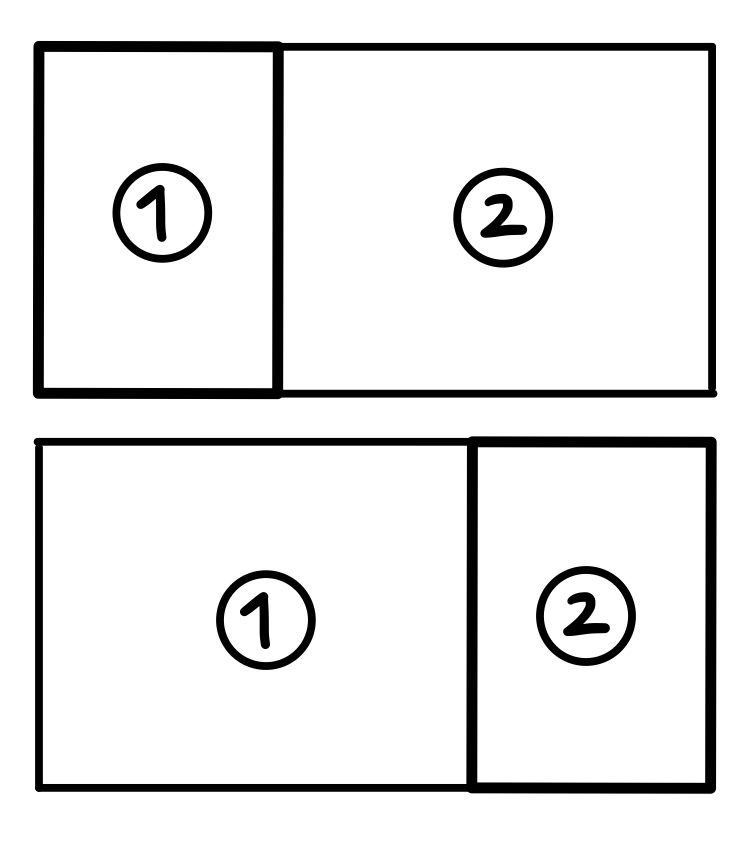
어 그럼 3x6일 땐 3x4랑 A, B, C 합치면 되는거 아냐? (11*3)*2 해서 66개네~
그리고 특별한 모양만 합치면 되는거 아냐?라고 하면 어림도 없다....

이런 경우는 위 그림의 1, 2번 위치를 바꾸더라도 중복될 수 밖에 없다.
문제는 이렇게 서로 중복되는 경우가 대부분이라는 것이다.
이 때 3x4에서 등장했던 특별한 형태를 이용할 수 있다.
다시 천천히 살펴보자,,,

이걸 case1이라고 하겠음.
너무 당연하게도 1번에는 ABC 밖에 들어갈 수 없다.
2번은 ABC 조합과 3x4의 특별한 모양을 넣을 수 있다.
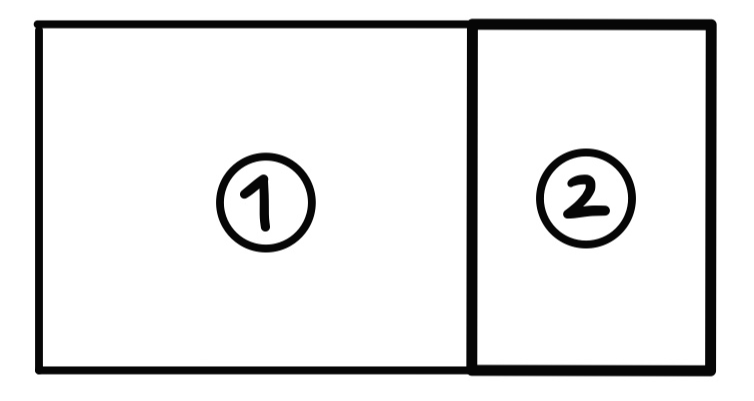
이건 case2라고 하겠음.
마찬가지로 2번에는 A, B, C 밖에 들어갈 수 없다.
1번은 ABC 조합과 3x4의 특별한 모양을 넣을 수 있는데...
1번을 ABC 조합으로 채워버리면 무조건 case1과 중복될 수 밖에 없다.
중복을 피하기 위해선 case2의 1번을 case1의 2번과 다르게 채워야 한다.
ABC 조합은 무조건 중복될 수 밖에 없으니 특별한 모양을 생각해보자.
case2의 1번을 특별한 모양으로 채우면 절대!!! 중복이 될 수 없다.

그러므로 case1 : 3*11 = 33, case2 : 2*3 = 6
33+6=39, 총 39가지가 발생한다.
끝이 아니다!!!!
또!!! 또^^~~ 예외가 있다.
잊으면 안된다 3x6만의 특별한 모양..
특별한 모양은 다행히 항상 2가지 씩만 등장한다.
찐찐막 3x6은 39+2=41개의 경우의 수를 가진다.
5. 3x8
3x8은 case가 3개로 늘어났다.
case1 : 3x6 + 3x2
case2 : 3x4 + 3x4
case3 : 3x2 + 3x6
case1은 단순하게 41*3=123 으로 구하겠다.
case2부터 중복을 생각해야 한다.
case1과 겹치지 않으려면 마지막 3x2를 ABC로 채우지 않으면 된다.
3x4 크기의 벽을 채울 때, 마지막 3x2를 ABC로 채우지 않으려면 특별한 모양을 사용할 수 밖에 없다..
따라서 case2는 11*2=22가 된다.
case3은 case1, 2를 피해야 한다.
case1과 겹치지 않기 위해서 마지막 3x2를 ABC로 채우면 안되고
case2와 겹치지 않기 위해서 마지막 3x4를 3x4 특별한 모양으로 채우면 안된다..
즉 3x6에서 발생한 특별한 모양 2개만 사용할 수 있다
case3 = 3*2 = 6
찐막으로 3x8은 123+22+6+2(3x8 특별한 모양)=153이 된다.
이제 드디어 점화식을 세울 수 있다.
방금 구한 N=8일 때로 생각해보자.
dp[8] = (dp[6]*dp[2]) + (dp[4]*2) + (dp[2]*2) + 2
그리고 위 식에서 숫자 8을 N으로 표현하고, +2를 바꿔보자
dp[N] = (dp[N-2]*dp[2]) + (dp[N-4]*2) + (dp[N-6]*2) + (dp[N-8]*2) + ··· + (dp[2]*2) + dp[0]*2
dp[0]에는 1을 넣어둘 것이다.
코드를 깨끗하고 편하게 짜기 위해서 저렇게 수정했다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
import java.util.Scanner;
public class BOJ_2133 {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int N = scan.nextInt();
int [] dp = new int[N+1];
dp[0] = 1;
for(int i=2; i<=N; i++) {
dp[i] = 3*dp[i-2];
for(int j=i-4; j>=0; j-=2)
//2 = 특별한 모양 2가지
dp[i] += dp[j]*2;
}
System.out.println(dp[N]);
}
}
|
cs |
정말 쉽게 봤다가.. 대갈 터진 문제ㅎ
모든 설명은 아래 블로그를 참고했다.
구글링 해서 다 뒤져봐도 여기 설명이 최고였음ㅠㅠ
[ 백준 2133 ] 타일 채우기 (C++)
백준의 타일채우기(2133) 문제이다. [ 문제 바로가기 ] [ 문제풀이 ] 3 x N 크기의 벽을 2 x 1 , 1 x 2 타일들로만 채울 때, 그 경우의 수를 구해야 하는 문제이다. 작은 수들부터 차근차근 만들어보면서
yabmoons.tistory.com
'Algorithm > BOJ' 카테고리의 다른 글
| [백준/BOJ/JAVA/정렬] 11004 K번째 수 (0) | 2021.10.03 |
|---|---|
| [백준/BOJ/JAVA/DP] 2011 암호코드 (0) | 2021.10.03 |
| [백준 알고리즘/C++/큐, 덱] 5430 AC (0) | 2021.07.09 |
| [백준 알고리즘/C++/큐, 덱] 1021 회전하는 큐 (0) | 2021.06.16 |
| [백준 알고리즘/C++/큐] 1966 프린터 큐 (0) | 2021.06.01 |