많은 데이터들을 효율적으로 관리하기 위해 자료구조와 알고리즘이 개발되었다
이 알고리즘의 성능을 수학적으로 표현하기 위해 빅오 표기법을 사용함
빅오로 시간 복잡도와 공간 복잡도를 나타낼 수 있음!
이 복잡도에는 몇 가지 규칙들이 있다
1. 입력값은 항상 0보다 크다 (입력값이 음수일 수 없음)
2. 입력값이 많을수록 더 많은 작업을 한다
3. 모든 상수를 삭제한다
: 어떤 알고리즘의 시간복잡도가 O(3n)이라면 3을 삭제한 O(n)이 해당 알고리즘의 시간 복잡도가 됨
4. 낮은 차수의 항들은 무시한다
: n과 n^2을 비교할 때, 어느 시점에선 n^2이 더 빠를 수 있지만
복잡도는 n이 무한으로 커진 경우를 가정해야 하기 때문에, 무조건 n^2가 더 오래 걸린다고 판단함
n^3 + n^2 + n 이라는 함수가 있을 때 n^3만 고려하면 됨
5. 시간/공간 복잡도에 log가 포함되는 경우 밑은 무시한다
6. 등호를 사용하여 표현한다
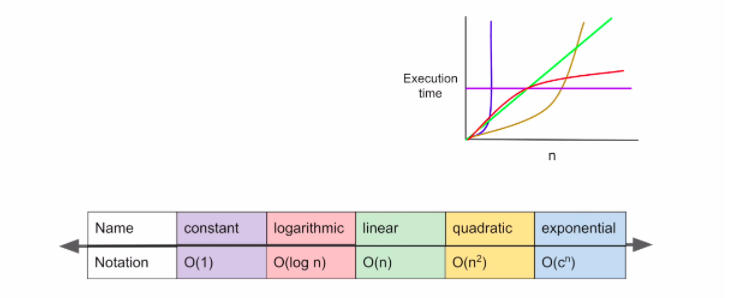
빅오 표기법
O(1) : 입력 자료의 수(n)에 관계없이 일정한 실행 시간을 갖는 알고리즘
(배열에서 특정 인덱스 찾기, 해시테이블 추가)
O(log n) : 초반엔 빠르지만 후반부 갈수록 시간이 증가함 (이진 탐색)
O(n) : 입력 자료의 크기가 N일경우 N 번만큼의 수행시간을 가짐 (연결 리스트 순회, 최댓값 찾기)
O(n log n) : 선형 로그형, 데이터 수가 2배 늘 때, 연산횟수가 2배 조금 넘게 증가함 (퀵, 병합정렬)
O(n^2) : 주로 2중 for loop를 사용하여 조합가능한 모든 쌍을 대상으로 함 (버블, 삽입 정렬)
O(n^3) : 3차형(cubic)
O(2^n) : 지수형 빅오, '지수적증가'는 과도한 연산 횟수 증가를 야기한다. (피보나치수열)
O(c^n) : 최악의 시간 복잡도 (재귀함수)
O(n!) : 계승(factorial)
이 정도만 알아보고 알고리즘까지 한 번 훑은 뒤에 다시 정리하기!
'Algorithm > 자료구조 & 알고리즘' 카테고리의 다른 글
| LinkedList (0) | 2021.07.27 |
|---|---|
| ArrayList (0) | 2021.07.27 |
| 다이나믹 프로그래밍 (0) | 2021.04.15 |
| 깊이 우선 탐색 DFS, 넓이 우선 탐색 BFS (0) | 2021.02.26 |
| 그리디 알고리즘 (0) | 2021.01.16 |